Многогранник Р называется однородным, если все его грани – правильные многоугольники, а любые две вершины могут быть переведены друг в друга при помощи симметрических преобразований так, что многогранник при этом переходит сам в себя. Гранями могут быть выпуклые и звездчатые правильные многоугольники.
Связный однородный многогранник без кратных вершин и ребер называется элементарным.
Как известно [1], конечная группа G самосовмещений P имеет неподвижную точку,
являющуюся центром описанной вокруг P сферы.
Элементами G могут быть только собственные вращения Bi вокруг инвариантной оси и вращательные симметрии Сi
представляющие собой произведение симметрии относительно плоскости и вращения вокруг прямой,
перпендикулярной плоскости симметрии. Если G содержит центральную симметрию I,
то любая вращательная симметрия может быть представлена в виде
Из всех конечных групп движений нас будут интересовать только группа самосовмещений куба S4 × {I} и группа самосовмещений икосаэдра A5 × {I}. Все остальные конечные группы либо являются подгруппами этих двух, либо соответствуют группам самосовмещений бесконечных серий призм и антипризм Dn × {I} [2].
В [3] был предложен перечень известных элементарных многогранников (см. также список однородных многограников), но полнота этого перечня не была доказана. В настоящей статье доказана
Метод доказательства этой теоремы заключается в следующем. Выбираем на сфере точку A0 и подвергаем ее всем преобразованиям из G. Количество образов A0 равно порядку G либо является делителем ее порядка. Выделим на сфере область Δ0, каждая точка которой расположена не дальше к точке A0, чем к любому из образов A0. Точки Ai, являющиеся образами A0, будут в свою очередь иметь соответствующие им области Δi. Все эти области равны между собой и покрывают в своей совокупности всю сферу. Каждой точке сферы соответствует единственная точка из Δ0. Для групп S4 × {I} и A5 × {I} Δ0 – прямоугольный треугольник. Будем называть Δ0 фундаментальным треугольником группы G. Выпуклая оболочка точек Ai есть выпуклый многогранник, имеющий G своей группой самосовмещений.
Определим векторы ri, с началом в центре сферы и концами в точках Ai, i = 0, 1, 2, ..., g-1, где g – порядок G. Если A0 находится на границе Δ0, то некоторые ri совпадают. Кроме того, определим векторы ρi с началом в A0 и концами в Ai, (i=1, 2, ..., g-1). У однородного многогранника P все ребра равны, а каждой вершине инцидентно ровно q правильных многоугольников, не обязательно одинаковых. Поэтому для того, чтобы точки Ai были вершинами однородного многогранника P, необходимо выполнение следующих условий:
Очевидно, что эти условия являются и достаточными для существования однородного многогранника. Действительно, многогранник с вершинами в точках Ai, ребрами которого являются векторы ρj и их образы, а гранями – многоугольники, удовлетворяющие условию 3), есть однородный.
Составляя все возможные скалярные произведения и приравнивая их попарно, мы получим уравнения для определения координат A0. Определяя углы между векторами ρj и проверяя выполнение условий 2) и 3), мы найдем все точки A0, образы которых служат вершинами однородных многогранников.
Идея этого метода принадлежит А. В. Погорелову.
В [4] были найдены все однородные многогранники, грани которых перпендикулярны инвариантным осям вращений. Следовательно, для доказательства Теоремы А нам остается найти многогранники, грани которых не все перпендикулярны осям вращений.
Преобразования из G, оставляющие грань многогранника P инвариантной, образуют группу H порядка h, которая является подгруппой группы G порядка g. Для группы S4 × {I} порядок g= 48, а для A5 × {I} порядок g= 120.
Пусть Гn – количество n - угольных граней однородного многогранника P, переходящих друг в друга при помощи преобразований из G. Назовём такие грани эквивалентными.
Теорема 1. Гn равно индексу группы G по подгруппе Н.
Доказательство. Преобразования, оставляющие плоскость грани многогранника P инвариантной, образуют группу F порядка f. В каждой такой плоскости располагаются компланарные, эквивалентные многоугольники, количество которых равно индексу F по подгруппе H, т. е. f / h. Количество же плоскостей, содержащих грань P, равно индексу группы G по подгруппе F, т. е. g / f. Порядок фактор группы G / H равен Гn = (g / f) * (f / h) = g / h, что и требовалось доказать.
Пусть P имеет N0 вершин. Тогда N0 является делителем g [5], т. е. g / N0 = m.
Следствие. Если вершине P инцидентно qn правильных n - угольников {n}*, то h = m n / gn.
Действительно, Гn = N0 qn / n [6]. Поэтому
Примечание *: в дальнейшем правильный n-угольник будем обозначать символом Шлефли {n}, а угольную звезду {n/d} – n.
Грань многогранника P, перпендикулярную k - кратной оси вращения, будем называть гранью типа γk (k = 2, 3, 4, 5). Если группа преобразований H, оставляющая грань инвариантной, имеет порядок h ≥ 3, то эта грань типа γk (k = 2, 3, 4, 5). Действительно, если H содержит только собственные движения, то утверждение справедливо. Если же H содержит несобственные движения, то, как известно [2], количество несобственных движений в H равно количеству собственных движений, т. е. в H есть вращения, отличные от тождественного.
Пусть теперь h = 2. Тогда H может иметь, кроме тождественного преобразования Е, еще одно преобразование β, такое, что β2 = Е. Таким преобразованием может быть: Bπ – поворот на угол π, С0 – отражение в плоскости или центральная симметрия I. В первом случае грань типа γ2, во втором и третьем случае – грани типа γ1 и γ0.
Если h=1, т.е. грань переводится в себя только тождественным преобразованием, то такую грань будем называть гранью типа γ0. Очевидно, что грани типа γ0, γ0 и γ1 могут быть гранями типа γk (k = 2, 3, 4, 5).
Для доказательства Теоремы А достаточно найти все элементарные однородные многогранники, имеющие грани типа γ0, γ0 или γ1.
Теорема 2. Если вершине элементарного однородного многогранника P инцидентно три грани (q = Σqi = 3), то все они типа γk (k = 2, 3, 4, 5).
Доказательство. Из следствия теоремы 1 имеем
| h qn = m n. | (1) |
| qn < q | (2) |
Пусть h = 1. Тогда из (1) следует, что qn = mn ≥ 3.
Но, согласно (2), qn < 3. Следовательно, при q = 3 многогранник P не может иметь
граней типа γ0.
Пусть h = 2.
Тогда (1) имеет вид 2qn = m n.
Это возможно только при qn = 2, m = 1, n = 4.
Если вершине многогранника P инцидентно три грани, из которых два квадрата,
то это может быть только призма [7]. Так как N0=g, то это может быть призма,
в основании которой лежит {24} или {60}, группы которых не совпадают с
группами S4 × {I} и A5 × {I}.
Если же в основании призмы лежит {n} при n ≠ 24 и n ≠ 60,
то это будет несвязный неэлементарный многогранник. Теорема 2 доказана.
Будем говорить, что P имеет ребро С или В, если инцидентные ему вершины преобразуются друг в друга соответственно несобственным или собственным движением. В частности, если С есть зеркальное отражение в плоскости, то ребро С0, а если В есть поворот на угол π, то ребро Вπ.
В дальнейшем нам потребуется следующая
Лемма. Элементарный однородный многогранник P, вершине которого инцидентно четыре грани, не может иметь двух граней типа γ1, инцидентных общему ребру С0.
Доказательство проведем отдельно для группы S4 × {I} и A5 × {I}. У икосаэдра все плоскости симметрии переходят друг в друга при преобразованиях из A5 × {I}. У куба же плоскости симметрии разбиваются на два типа. Три из них проходят через середины ребер и не содержат вершин, а остальные шесть содержат по два ребра и четыре вершины куба. Обозначим их через L3 и L6 соответственно. Если P имеет N0 = g, то ни одна плоскость симметрии не проходит через вершины P.
В случае группы S4 × {I}, согласно теореме 1, эквивалентных граней типа γ1, должно быть 24. Предположим, что утверждение леммы неверно. Тогда каждой вершине P инцидентно 2 либо 3 грани типа γ1, т. е. qn = 2, 3.
Докажем, что N0 = g. Как известно [6], Гn = qn N0 / n,
или
| n Гn = N0 qn. | (3) |
Пусть грань типа γ1 перпендикулярна плоскости L6. Каждой плоскости L6, согласно теореме 1, перпендикулярны 4 эквивалентные грани типа γ1. В каждой такой плоскости лежит четырехкратная ось вращения и перпендикулярная ей двукратная ось. Поворот вокруг этих осей на угол π переводит эту плоскость в себя. Если эквивалентные грани типа γ1 инцидентны общему ребру С0, то это ребро перпендикулярно двукратной или четырехкратной оси вращения и, следовательно, полностью содержится в одной из плоскостей симметрии, что невозможно.
Пусть теперь грань типа γ1 перпендикулярна плоскости L3. Каждой плоскости L3 перпендикулярно восемь эквивалентных граней типа γ1. Каждая такая плоскость содержит две взаимно перпендикулярные четырехкратные оси и две взаимно перпендикулярные двукратные оси. Угол между четырехкратной и двукратной осью равен π/4. Грани типа γ1, перпендикулярные плоскости L3, образуют пояс, сечение которого этой плоскостью есть {8}, {8/3} или {8/2}. Нетрудно убедиться, что в первых двух случаях плоскость симметрии проходит через вершины P, что невозможно. В последнем случае грани взаимно перпендикулярны и образуют два замкнутых пояса. Если n = 4, то это просто кубы, а P – неэлементарный многогранник. Если n = 6, то не существует вершинной фигуры с данными условиями.
Вершинной фигурой мы называем плоский многоугольник, вершины которого есть концы ребер, исходящих из данной вершины многогранника P, а стороны — диагонали (вершинные фигуры) граней, инцидентных данной вершине. Вершинной фигурой мы часто будем пользоваться в дальнейшем, характеризуя строение многогранника в окрестности его вершины.
Таким образом, для группы S4 × {I} лемма справедлива.
В случае группы A5 × {I}, согласно теореме 1, эквивалентных граней типа γ1, должно быть 60. Уравнение (3) дает следующие решения: qn=2, n=4, N0=120; qn=3, n=3, N0=60; qn=3, n=6, N0=120. Мы получаем антипризму при N0 = 60. В остальных случаях плоскости симметрии не могут проходить через вершины P. Каждой из пятнадцати плоскостей симметрии перпендикулярно четыре эквивалентные грани типа γ1. В каждой плоскости симметрии лежат две двукратные оси вращения. Пусть две грани типа γ1 имеют общее ребро С0. Тогда, как и в случае группы S4 × {I}, это ребро перпендикулярно двукратной оси. Так как через двукратную ось проходят две взаимно перпендикулярные плоскости симметрии, то одна из них должна полностью содержать ребро С0, т.е. проходить через вершины P. Лемма доказана полностью.
Теорема 3. Если вершине элементарного однородного многогранника P инцидентно четыре грани (q = 4), то все они типа γk (k=2,3,4,5).
Доказательство. В [8] были найдены все однородные многогранники с неотрицательной эйлеровой характеристикой χ=N0-N1+N2, где N0, N1, N2 – соответственно количество вершин, ребер и граней P. Если q = 4, то N1= 2N0 и для χ<0 имеем N2<N0 ≤ g. Отсюда, согласно теореме 1, сразу следует, что P не может иметь граней типа γ0. Если N0 ≤ g/2, то P не может иметь граней типа γ0 и γ1. Поэтому доказательство теоремы достаточно провести для многогранников с χ < 0 и количеством вершин, равным порядку группы.
Пусть P имеет грань типа γ0. Согласно теореме 1 и неравенству (3) вершине многогранника P могут быть инцидентны следующие грани типа γ0: 1) три шестиугольника и 2) два квадрата. В первом случае из четырех граней при вершине P три проходят через центр сферы, что невозможно. Во втором случае два квадрата должны перемежать две другие грани, не имеющие ребер С0. Таких граней должно быть меньше g/2. Для группы S4 × {I}, согласно теореме 1, таких граней нет. Для группы A5 × {I} такими гранями могут быть только два шестиугольника. Так как квадраты вписаны в большой круг сферы, описанной вокруг P, то шестиугольник вообще не может быть вписан в эту сферу. Следовательно, при q = 4 многогранник P не может иметь граней типа γ0.
Пусть P имеет грань типа γ1. По теореме 1 вершине многогранника P могут быть инцидентны два квадрата или три шестиугольника типа γ1. Если вершине инцидентно три шестиугольника, то четвертая грань согласно лемме должна иметь все ребра С0. Следовательно, она должна быть четноугольником типа γk (k=2,3,4,5). Если вершине инцидентно два квадрата типа γ1, то по лемме либо каждая из двух других граней имеет ребра С0, но не обязательно все, либо одна из них имеет все ребра С0, а вторая совсем не имеет таких ребер. Поэтому, если вершине P инцидентно четыре грани и среди них есть типа γ1, имеющие общее ребро, то все грани P – четноугольники.
Докажем теорему для группы S4 × {I}.
Пусть в вершине P сходится три шестиугольника типа γ1. Из (1) и (3) следует, что четвертой гранью может быть: 1) квадрат типа γ2 с ребрами С0, 2) шестиугольник типа γ2 с ребрами С0 и 3) восьмиугольник типа γ4 с ребрами С0. Второй случай невозможен по (2). Шестиугольники типа γ1 могут быть перпендикулярны либо плоскости L3, либо плоскости L6 и чередуются с гранями типа γk (k=2,4). Плоскости L3 перпендикулярно четыре восьмиугольника типа γ4 или четыре квадрата типа γ2. Следовательно, в первом и в третьем случае только 12 из 24 шестиугольников перпендикулярно плоскостям L3. В каждой плоскости L6 лежит одна двукратная и одна четырехкратная ось. Каждой из шести плоскостей L6 перпендикулярно по два шестиугольника типа γ1. Это невозможно.
Пусть вершине многогранника P инцидентно по два квадрата типа γ1, имеющих общее ребро. Из (1) и (3) получаем, что двумя другими гранями могут быть: 1) {4} типа γ2 с ребрами С0 и {6} типа γ3 с ребрами С0; 2) {4} типа γ2 с ребрами С0 и {8} типа γ4 с ребрами С0, 3) {6} типа γ3 с ребрами С0 и {8} типа γ4 с ребрами С0; 4) два {8} типа γ2, имеющие через одно ребра С0. В первых трех случаях из каждой вершины P исходит три ребра С0. Из простых геометрических рассуждений видно, что четвертое ребро Вπ. Следовательно, оно перпендикулярно двукратной или четырехкратной оси вращения. Квадраты типа γ1 образуют замкнутый пояс, их общие ребра Вπ. Многогранник P вписан в сферу, поэтому все ребра Вπ этого пояса параллельны. В силу структуры плоскостей симметрии это возможно лишь в случае, когда все ребра Вπ параллельны четырехкратной оси. Но тогда все эти ребра С0, а квадраты типа γk (k=2,4). В четвертом случае восьмиугольники типа γ2 инцидентны квадратам по ребрам С0. Так как {8} перпендикулярен к плоскости L3 и плоскости L6, то и квадраты типа γ1 перпендикулярны плоскостям симметрии различных типов, что невозможно.
Пусть теперь квадраты типа γ1 разделены другими гранями. Такими гранями могут быть: 1) два {8} типа γ2, имеющие через одно ребра С0; 2) {3} типа γ3 с ребрами В и {8} типа γ4 с ребрами С0; 3) {4} типа γ4 с ребрами В и {6} типа γ3 с ребрами С0; 4) {4} типа γ4 с ребрами В и {8} типа γ4 с ребрами С0. Это легко получается из (1) и (3) с учетом того, что χ < 0 и в одной плоскости не может лежать более восьми вершин многогранника P [5]. Pассматривая замкнутые пояса из граней P, перпендикулярные плоскостям L3 и L6, мы, как и выше, приходим к выводу, что многогранников с данными гранями нет.
Итак, для группы S4 × {I} теорема доказана.
Рассмотрим группу A5 × {I}. В каждой плоскости симметрии икосаэдра лежат две взаимно перпендикулярные двукратные оси, две трехкратные и две пятикратные оси вращения.
Пусть вершине многогранника P инцидентно три {6} типа γ1. Тогда на основании теоремы 1 граней типа γ1 – 60. Из (1), (2) и (3) следует, что четвертой гранью при вершине может быть {4} типа γ2 с ребрами С0 или {10} типа γ5 с ребрами С0.



Аналогично последнему случаю с тремя шестиугольниками при вершине P опровергаются случаи 4), 6) и 7). В случае 5), рассматривая замкнутый пояс из квадратов типа γ1 и γ2 и считая радиус описанной сферы двумя различными способами, приходим к двум неравным значениям для R.
Осталось рассмотреть два последних случая при условии, что квадраты типа γ1 не имеют общего ребра.
В случае 9) вершинам одного {12} инцидентно двенадцать или шесть {12} типа γ3. Пусть два {12} имеют одну общую вершину. Для каждого {12} из двадцати существует параллельный ему {12}. Поэтому из вышеупомянутых двенадцати {12} по крайней мере две пары параллельны. Так как все они вписаны в сферу, то эти {12} образуют с инцидентным им {12} угол, равный π/2, т.е. угол между двумя трехкратными осями равен π/2, что невозможно. Пусть два {12} имеют две общие вершины, не инцидентные одному ребру. Тогда шесть {12} должны образовать с исходным {12} равные двугранные углы. Следовательно, должны существовать шесть трехкратных осей, образующих равные углы с данной трехкратной осью. Это невозможно.
Подобные рассуждения в случае 8) приводят нас к известным многогранникам, вписанным в усеченный куб с группой S4 × {I}, грани которых типа γk (k=2, 3, 4). Новых элементарных многогранников мы не получаем.
Теорема 3 полностью доказана.
Расположим куб с ребром 2 в прямоугольной системе координат так, чтобы начало координат совпало с центром куба,
а грани его были перпендикулярны координатным осям.
В выбранной таким образом системе координат вершины куба имеют координаты (1; 1; 1), (-1; 1; 1), (-1; -1; 1),
(1; -1; 1), (1; 1; -1), (-1; 1; -1), (1; -1; -1) и (-1; -1; -1),
а плоскости симметрии куба записываются уравнениями: X=0, Y = 0, Z = 0
(плоскости L3)
и
X=Y, X=-Y, X=Z, X=-Z, Y=Z и Y=-Z
(плоскости L6).
Плоскости симметрии разбивают грани куба на сорок восемь треугольников Δi.
Выберем среди этих треугольников тот, для координат каждой точки которого выполняется неравенство
| 0 ≤ X ≤ Y ≤ Z = 1. | (4) |
Выберем внутри Δ0 точку A0 (X; Y; 1). Образы этой точки Ai ∈ Δi, i = 0, 1, ..., 47. Координаты некоторых точек Ai отличаются от координат A0 только знаком, другие только порядком, остальные и тем и другим. Если возьмем точку A0 на границе фундаментального треугольника Δ0, то некоторые образы Ai совпадают. Границу Δ0 составляют прямые X = 0, Y = 1 и X = Y (при Z = 1). Число образов точки, взятой на границе Δ0, является делителем порядка группы. В частности, в вершинах Δ0 совпадают по 8, 6 и 4 образа A0. Эти точки определяют вершины правильных и квазиправильного многогранников с группой S4 × {I}. Точка (0; 0; 1) и ее образы служат вершинами октаэдра, точка (1; 1; 1) – куба и (0; 1; 1) – кубооктаэдра.
Каждая точка A0(X; Y; 1) и ее образы Ai служат вершинами многогранника,
порождающего группу S4 × {I}.
Для того, чтобы этот многогранник был однородным, необходимо еще равенство всех его ребер.
Это соответствует равенству скалярных произведений по крайней мере трех векторов ri
с началом в центре куба и концами в точках Ai на вектор r0.

Для нахождения точек A0(Х; Y; 1) с требуемыми свойствами мы предварительно приравняем скалярные произведения по два. Результаты приведены в таблице 2.
Таблица 2.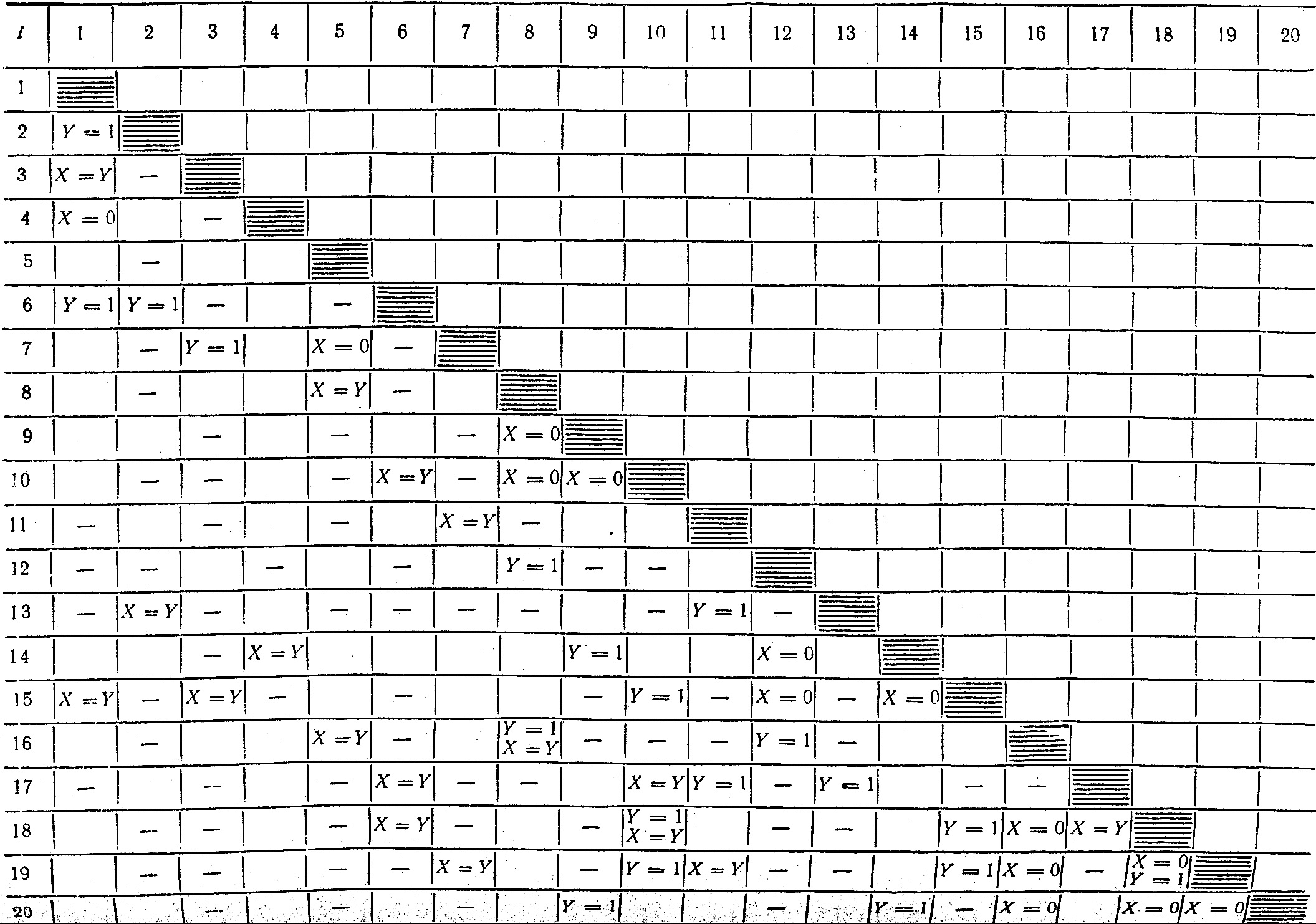
Прочерки в таблице 2 обозначают, что скалярные произведения не равны ни для одной точки из Δ0, либо равны только в вершинах Δ0, т.е. в точках (0; 0; 1), (1; 1; 1) и (0; 1; 1). Незаполненные клетки на пересечении двух скалярных произведений обозначают, что эти скалярные произведения равны вдоль некоторых линий в Δ0. Это либо прямые линии, либо кривые второго порядка. В таблице отмечены только те скалярные произведения, которые совпадают на границе фундаментального треугольника Δ0. Точка A0(Х; Y; 1), удовлетворяющая только двум скалярным произведениям, не может определять вершин элементарного однородного многогранника, имеющего грани типа γ0, γ0 или γ1. Кратность двух скалярных произведений не превышает четырех. Согласно теоремам 2 и 3, элементарные однородные многогранники при q ≤ 4 имеют все грани типа γk, k = 2, 3, 4. Поэтому для определения точек с кратностью больше четырех будем приравнивать Θi по три.
Найдем точки A0, расположенные внутри Δ0. Приравнивая Θi по три, мы получаем уравнения не выше четвертой степени для определения координат A0. В таблице 3 приведены результаты решений этих уравнений с учетом того, что кратность A0 больше четырех. Таких точек оказалось только семь. Остальные 32 точки имеют кратность меньше пяти.
Таблица 3.
Для того, чтобы многогранник с вершинами в исходной точке и ее образах был однородным, необходимо, чтобы ее грани были правильными многоугольниками. Определим углы между ребрами многогранника, инцидентными его вершине A0. Направление этих ребер определяют векторы ρi = ri - r0. Из семи интересующих нас точек только две определяют векторы ri, удовлетворяющие условиям 1), 2), 3).


Итак, кроме перечисленных в [4] элементарных однородных многогранников, грани которых перпендикулярны инвариантным осям куба, существует только один элементарный однородный многогранник с группой S4 - плосконосый куб.

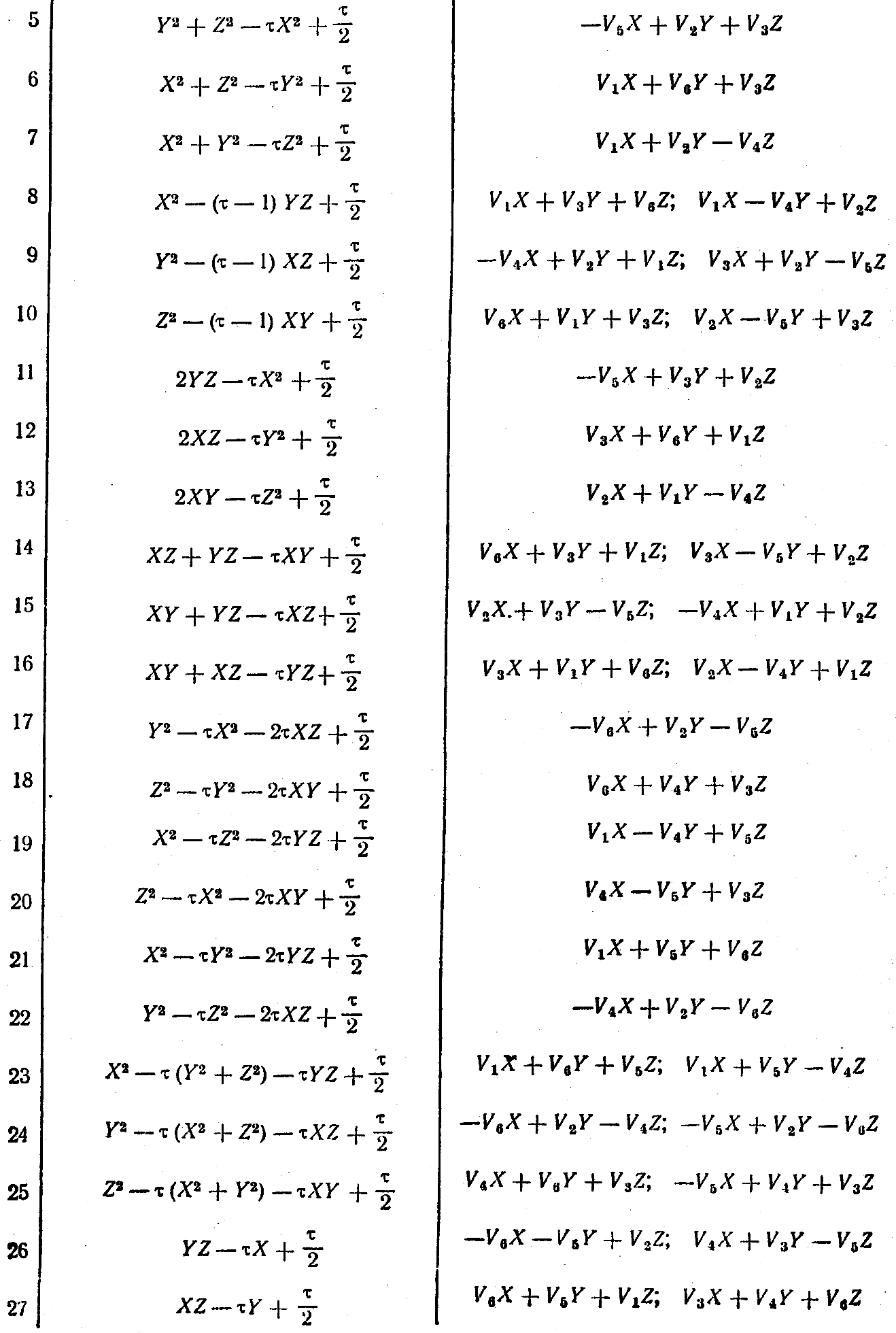
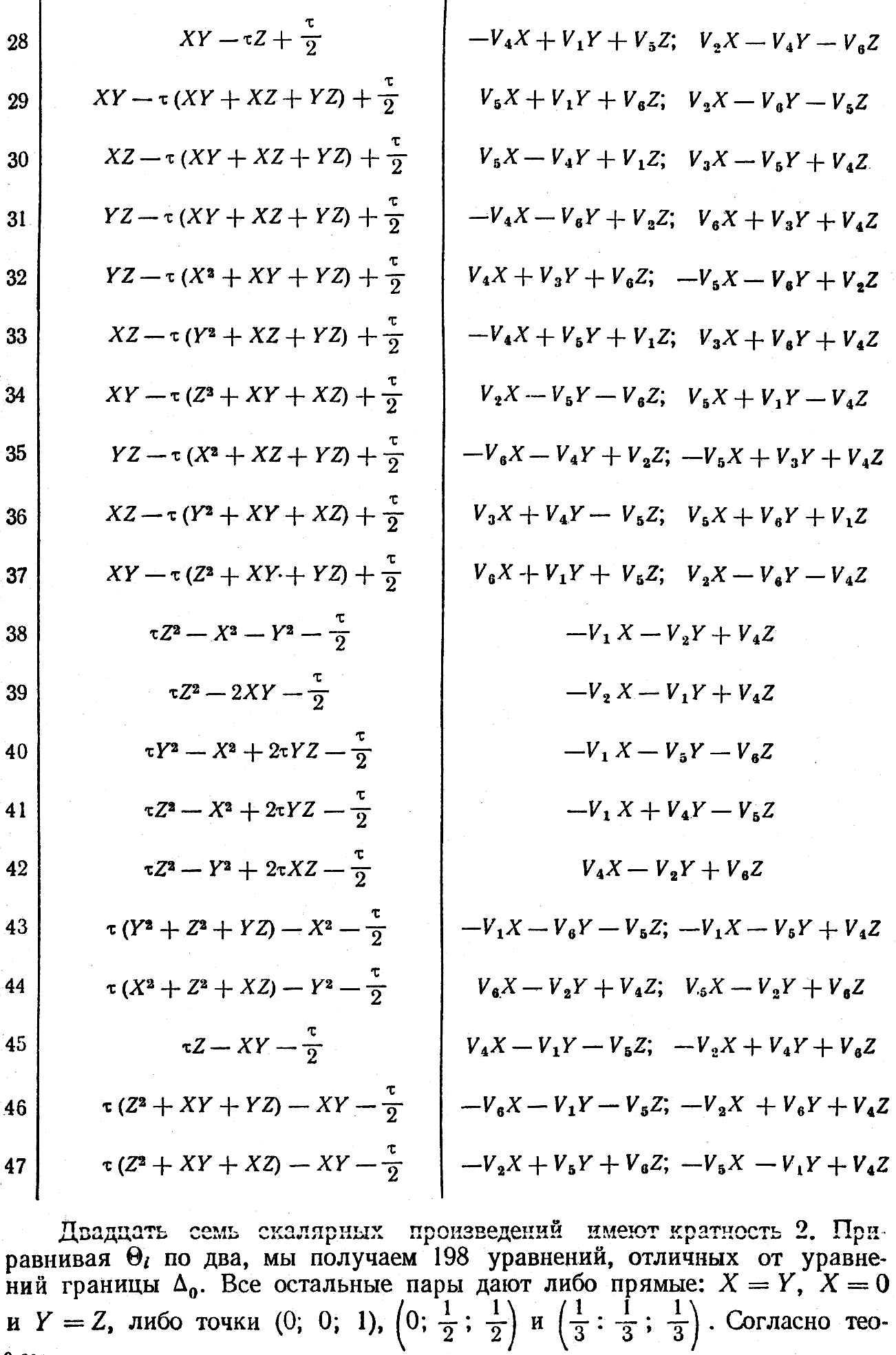

Таким образом, существует одиннадцать элементарных однородных многогранников (см. №18, №66, №67, №68, №69, №70, №71, №72, №73, №74, №75) с группой A5 × {I}, среди граней которых есть грани типа γ0, γ0 или γ1.
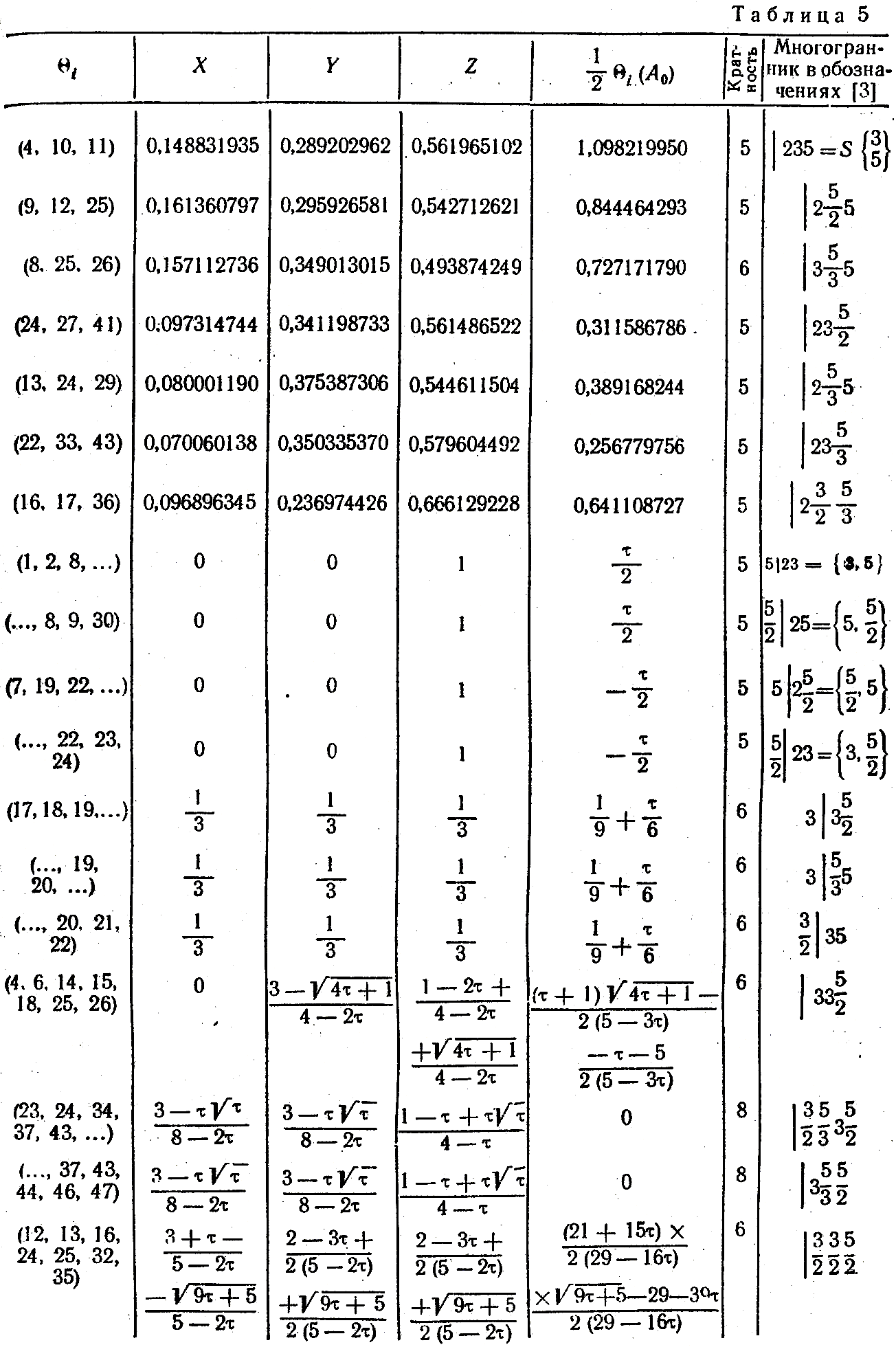
Используя результаты настоящей статьи и [4], мы приходим к выводу, что перечень элементарных однородных многогранников, приведенный в [3, табл. 7], (см. также следующую таблицу), полон. Таким образом, Теорема А полностью доказана.
В заключение автор выражает искреннюю благодарность А. И. Медянику за ряд ценных советов и помощь при оформлении этой статьи, а также Ю.Л. Подпалову и В.И. Хатунцеву за численное решение уравнений на ЭВМ.